

2024-10-30 12:21 点击次数:149
走进一个充满欢呼声的体育场,空气中充满了对即将到来的两支强大足球队之间对决的期待。一个引人入胜的问题浮现出来:我们可以在比赛开始之前预测比赛的结果吗? 本文提出了一个基于概率和统计的模型,通过考虑每支队伍的进攻和防守能力,以及主客场因素,来预测比赛的可能结果。

现在有20只球队,每支球队在该赛季的进球与失球情况已知,当其中两支球队相遇,我们如何预测两队的胜负或者更确切的两队的比分值呢?
这是20只队伍的历史数据:
队伍积分进球数失球数
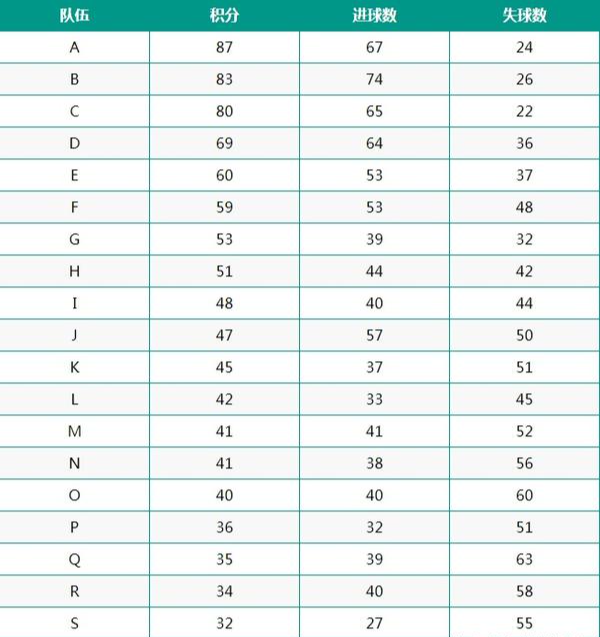
接下来我们开始建模,模型的核心逻辑是一个队伍在一场比赛中的进球数量等于主场因素、进攻优势与防守弱势的乘积。使用该指标我们可以预测进球数量对应的概率。
对于每支队伍,进攻指标定义为其进球数除以整个联赛的平均进球数;防守指标则定义为其失球数除以联赛平均失球数。同时研究表明,主场队伍倾向于表现得更好,因此我们将引入主场因素来调整预测。
为了进一步细化这个模型,我们首先需要计算整个联赛的平均进球数和平均失球数。这些平均值将用于计算每支队伍的进攻和防守指标。以此为基础,我们可以预测任意两支队伍相遇时的比赛结果。
计算联赛的平均进球数和平均失球数
首先,我们计算整个联赛的总进球数和总失球数,然后除以队伍数量,得到平均进球数和平均失球数。
平均进球数的计算

平均失球数的计算

计算进攻和防守指标
对于每支队伍,进攻指标和防守指标的计算如下:

这两个指标帮助我们理解每支队伍相对于联赛平均水平的进攻和防守能力。
主客场因素的考虑
研究显示,主场队伍通常表现得更好。为了考虑这一因素,我们可以对主场队伍的进球预期进行调整。例如,我们可以将主场队伍的进攻指标乘以一个大于1的系数,而客场队伍进攻指标乘以一个较小的系数。这里我们取主场系数为1.36,客场系数为1.06.
根据上述计算得出的预期进球数,我们可以使用泊松分布来预测每支队伍在比赛中进球的概率分布。泊松分布是一种用于估计在给定时间内发生特定数量事件的概率的分布,非常适合用于预测足球比赛中的进球数。一些读者可能对泊松分布不太熟悉,我们这里举个例子来进行说明。
泊松分布的基本概念源于18世纪法国数学家泊松的研究,它描述了在一定时间间隔内发生某种随机事件的次数的概率分布。在足球比赛的背景下,这种随机事件可以是进球的发生。假设我们知道一个队伍的预期进球数(即平均进球数),泊松分布可以帮助我们计算这个队伍在比赛中进0球、1球、2球等不同数量球的具体概率。
例如,如果队伍A对队伍B的比赛中,队伍A的预期进球数为1.122。使用泊松分布,我们可以计算队伍A在比赛中进球数为0, 1, 2, 3等的概率。计算公式如下:

假设我们计算队伍A进O球的概率:
同样,我们可以计算队伍A进1球的概率:
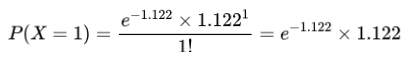
以此类推,我们可以计算进2球、3球等的概率。
我们可以画出图像表示不同进球数对应的概率:
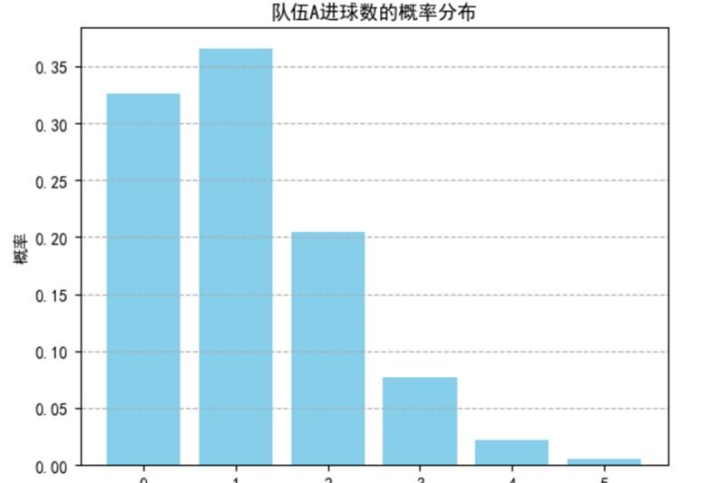
如图所示,队伍A在比赛中进球数的概率分布被清晰地展示出来。概率分布显示,队伍A最有可能进0球或1球,其次是进2球的概率,进球数越多的概率逐渐降低。这种分布是泊松分布的典型特征,它揭示了在给定预期进球数(本例中为1.122)的情况下,实际进球数分布的情况。
现在我们来预测两支球队比赛的结果。我们就采用文章最开始给出的那张进球表,来预测A队与B队(其中A队是主场)的比赛结果。
通过对两支队伍分别进行泊松分布计算,我们可以得到它们在比赛中进球数的概率分布。结合这些概率,我们可以估计不同比分发生的概率,进而预测比赛结果(胜、负、平)。
首先计算联赛的平均进球数和平均失球数:
联赛的平均进球数和平均失球数均为45.95。这是通过将所有队伍的进球数和失球数分别相加后除以队伍的总数得到的。
计算进攻和防守指标:
A队的进攻指标 = A队的进球数 / 平均进球数 = 67 / 45.95 = 1.458。
A队的防守指标 = A队的失球数 / 平均失球数 = 24 / 45.95 = 0.522。
B队的进攻指标 = B队的进球数 / 平均进球数 = 74 / 45.95 = 1.610。
B队的防守指标 = B队的失球数 / 平均失球数 = 26 / 45.95 = 0.566。
主客场因素的考虑:
假设A队是主队,我们采用主场系数1.36;B队是客队,采用客场系数1.06。
计算预期进球数:
A队对B队的预期进球数 = 主场系数 * A队进攻指标 * B队防守指标 = 1.36 * 1.458 * 0.566 = 1.122。
B队对A队的预期进球数 = 客场系数 * B队进攻指标 * A队防守指标 = 1.06 * 1.610 * 0.522 = 0.892。
据去哪儿平台数据,2024年十一旅游市场呈现“量涨价跌”趋势,国内机票价同比降20%,国庆假期前夕,部分线路或景点还有低价机票、酒店可捡漏。
使用泊松分布计算比赛结果的概率:
根据泊松分布公式,我们可以计算出在给定的预期进球数下,A队和B队进球0, 1, 2球的概率。我现在将两队不同进球数的概率分布绘制在一张图中:
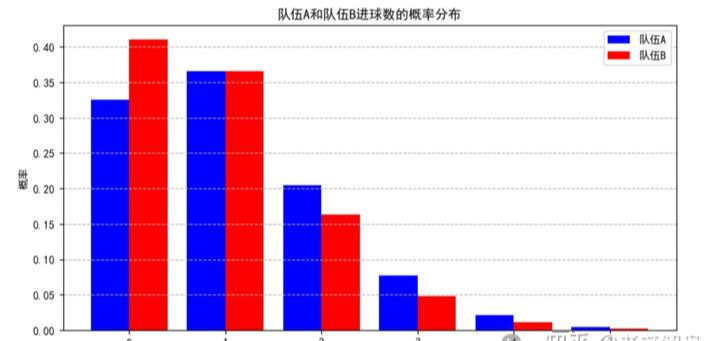
结合A队和B队的进球概率,我们可以估计不同比分发生的概率,如0-0、1-0、2-1等。这通过将A队和B队各个进球数的概率相乘来实现,例如A队进1球且B队进0球的概率就是两者相应概率的乘积。
利用泊松分布计算的比分概率如下:
比分0-0的概率约为13.35%。
比分1-0的概率约为14.98%。
比分2-0的概率约为8.40%。
比分0-1的概率约为11.90%。
比分1-1的概率约为13.36%。
比分2-1的概率约为7.49%。
比分0-2的概率约为5.31%。
比分1-2的概率约为5.95%。
比分2-2的概率约为3.34%。
这些概率提供了对可能出现的不同比分的估计,从而帮助我们预测比赛结果。例如,最可能的结果是比分为1-0,其次是比分0-0和1-1,这表明比赛可能会相当紧张和竞争激烈。
在这个统计模型的帮助下,我们不仅能预测比赛的可能结果,还能深入了解每支球队的进攻和防守能力。这种方法允许我们用数据和概率来解读比赛,而不仅仅是依赖直觉和主观判断。通过精确的计算和分析,我们可以更好地理解比赛的不确定性,并尝试预测那些关键的比赛时刻。
当然没有任何预测模型能保证百分之百的准确率,因为足球比赛的结果受到许多不可预测因素的影响体育荣耀,如天气条件、球员受伤或红牌等突发事件,但这种基于统计的方法无疑为比赛结果的预测提供了科学依据